The algorithms taught to computer science students haven't changed all that much in the last several decades, but the machines that these algorithms run on have changed a great deal. Each of these algorithms is analyzed and justified based on a model of the machine running the algorithm. The analysis is often in terms of asymtotic behavior (usually described as the behavior on large problems)
This paper claims that the machines we run today do not resemble, in performance, the models being used to justify traditional algorithms. In fact, today's caches and memory systems seem to reward sequential memory access, but may actually penalize memory patterns that seem to have considerable locality of reference. This behavior is especially noticable for very the kinds of very large problems that are driving us to 64-bit architectures.
Traditional classes that teach analysis of algorithms and data structures use a model, often an implicit one, of how an algorithm performs on a computer. This model often has a uniform memory model, where loads all take the same time and stores all take the same time. The cost of making function calls, allocating memory, doing indexing computations, loading and storing values is often ignored or dismissed as unimportant.
A couple of decades ago, numerical algorithms were analyzed in terms of FLOPs (floating point operations). Various schemes were used (some counted loads and stores, some treated divide as more expensive than multiply). Over time, it became clear that the FLOP count for an algorithm had only the most tenuous connection with the running time of the algorithm, and the practice fell into disuse.
I hope to awaken a doubt in you that such traditional techniques as linked lists, structures, binary trees, and "divide and conquer" algorithms are always good for large problems on today's machines. Let's start with some simple measurements. You are encouraged to try this at home on your own computer.
Most modern computers have CPU cycle counters. These have the advantage that, for desktop machines, they can produce extremely accurate and repeatable timings. The times in this paper are all obtained using cycle counters.
However, there are disadvantages. There appears to be no portable way of turning cycle counts into clock time (e.g., determining the clock speed of your computer), or even getting at the cycle timer itself. In the case of laptops, the situation is quite bizarre--most laptops run faster when plugged into the wall than they do when running on batteries. Also, laptops tend to slow down when they get hot (i.e., when they are doing work!). So running tests on laptops can be misleading and the data can be quite noisy. All the data in this paper was gathered from desktop machines.
So please try this at home, but preferably not on a laptop. This article gives all the code you will need to replicate this data on an Intel-based Linux system using gcc.
I used a simple C++ class to do the basic timing. There are two methods of interest: tic and toc. Calling tic reads the cycle counter and saves the value; calling toc reads the counter again and returns the difference. The CPU timer class is:
class CYCLES
{
long long var;
public:
CY(void){};
~CY(void){};
void tic(void);
long long toc(void);
};
static long long int cycle_time;
static void tsc(void)
{
__asm__ volatile ("rdtsc" : "=A"(cycle_time));
}
void CYCLES::tic(void)
{
tsc();
var = cycle_time;
}
long long CYCLES::toc(void)
{
tsc();
return( cycle_time - var );
}
The first program examines how the process of summing a million double precision numbers is affected by the order in which we do the summation. We can add the numbers sequentially through memory. Or we can add every other number, then come back and get the numbers we missed on a second pass. Or add every third number, and then make two additional passes to get the ones we miss. The relevant part of the program is
CYCLES c; // cycle counter #define N 1000000 double a[N]; // the array to be summed // initialize a for( int i=0; i<N; ++i ) a[i] = 1.0; double S = 0.; long long t; // the cycle count // time a sum of stride s c.tic(); for( int i=0; i<s; ++i ) for( j=i; j<N; j += s ) S += a[j]; t = c.toc();
In fact, the data to be presented are the average of ten runs, and cover strides from 1 to 1040. The cycle counts are normalized so that the stride 1 case is 1.0.
This example is not as contrived as it may appear to be, since it simulates array access patterns in large two-dimensional arrays. For example, stride 1000 simulates the reference pattern in a 1000x1000 double precision array where the "bad" dimension varies most rapidly (The "bad" dimension in C is the first one, while in FORTRAN and MATLAB it is the second one). Here is the data for an AMD 64-bit processor, when the program is compiled unoptimized.
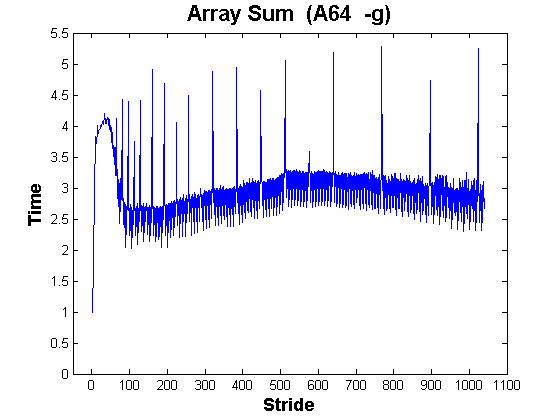
Notice that stride 1 is the fastest, as we might expect. But beyond that, there are some unintuitive features of this graph:
Actually, the spikes, while striking, are probably the feature of these graphs that is easiest to understand. They probably arise from the way caches are designed in most modern CPU's. When an address reference is made, some bits from the middle of that address are used to select a portion of the cache to search for a match, to save time and power. Unfortunately, this means that when the stride is close to a high power of two, only a small portion of the available cache space is being used. It is as if the effective cache size is a tiny fraction of that available in the unit stride case. This effect happens, with somewhat different numerology, with each of the caches (modern systems have two or three).
What is surprising, especially in the later data, is the magnitude of this effect...
The above graph involved unoptimized code. If we optimize (gcc -O4), we get:
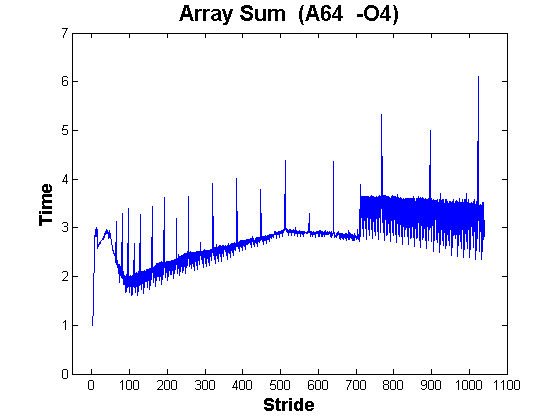
Optimization does not change the essential shape or properties of the curve, although the spikes are a bit higher. This effect is largely the result of the code for unit stride being a bit faster (recall that the graphs are normalized so that unit stride is 1.0).
We can also collect data on a 32-bit AMD processor:
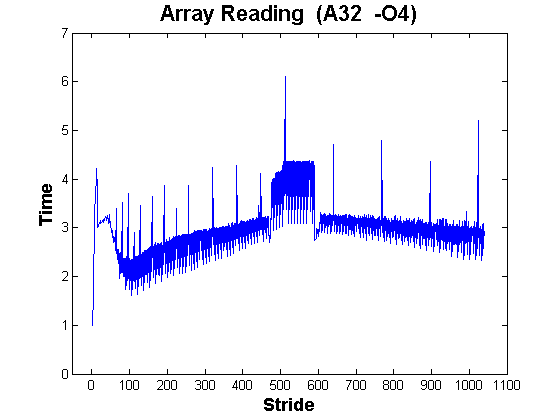
Notice that the shape of the curve is similar, but the spikes are closer together. There is also a strange "hump" around 512 which appeared on multiple runs (this doesn't mean it isn't an artifact!). The unoptimized version of this test on the 32-bit AMD system also had a hump that was lower and broader. The 64-bit AMD may show signs of a smaller hump centered around 1024.
Here is the curve for an Intel 32-bit System.
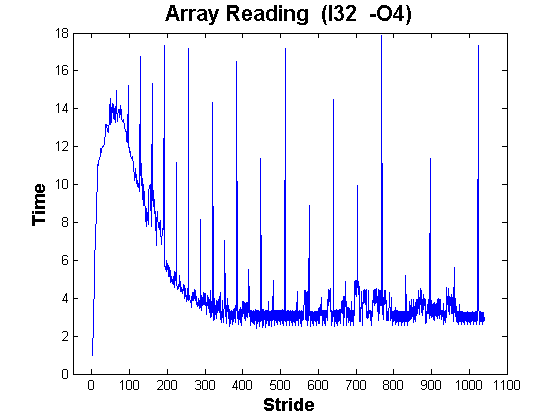
Note that the behavior for small strides is much worse than the AMD machines, but there is no sign of "the hump". The spikes are closer together, probably because the caches are smaller.
We can run a similar test on writing data. In fact, we do not need to initialize the array, so the code is simpler:
CYCLES c; // cycle counter #define N 1000000 double a[N]; // the array to be written long long t; // the cycle count // time writing N elements with stride s c.tic(); for( int i=0; i<s; ++i ) for( j=i; j<N; j += s ) a[j] = 1.0; t = c.toc();
Here are the results for a 64-bit AMD machine:
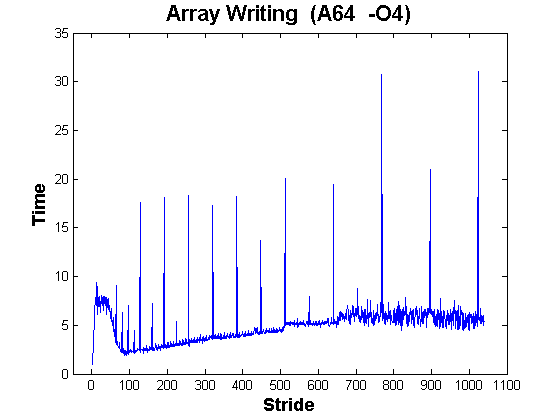
At first glance, the data appears smoother (except for the spikes), but this is an illusion, because the scale is much larger. In this case, the worst peaks are up to 30x the unit stride times. Once again, the peaks appear at strides that are powers of two.
Here is the 32-bit AMD data:
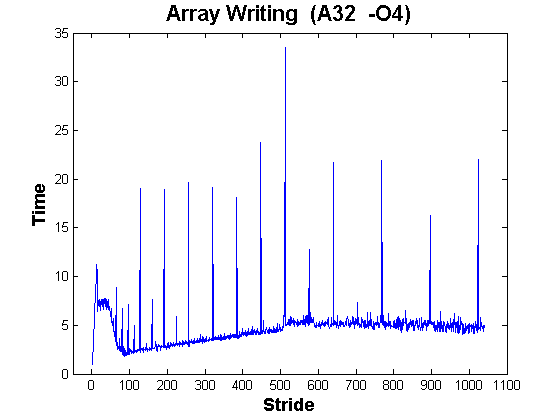
Again the peaks appear at powers of two, and again are up to 30x worse than unit stride. The Intel 32-bit graphs for reading and writing are quite similar.
The programs for summing and writing data are "worst case" examples for cache behavior, because we touch each data element exactly once. We can also examine what happens when we write data repeatedly. By modifying our test case slightly, we can write only 1000 elements out of the million element array, but write element 1000 times. Once again, we vary the strides of the 1000 elements. Note that for all strides, only 8000 bytes are written. The program looks like:
CYCLES c; // cycle counter #define N 1000000 double a[N]; // the array to be written long long t; // the cycle count // time writing N elements with stride s // note: N must be bigger than 999*s+1 c.tic(); for( int i=0; i<1000; ++i ) for( j=k=0; k<1000; j += s, ++k ) a[j] = 1.0; t = c.toc();
We can be forgiven for hoping that this amount of data can fit comfortably into the caches of all modern machines. But here are the 64-bit AMD results:
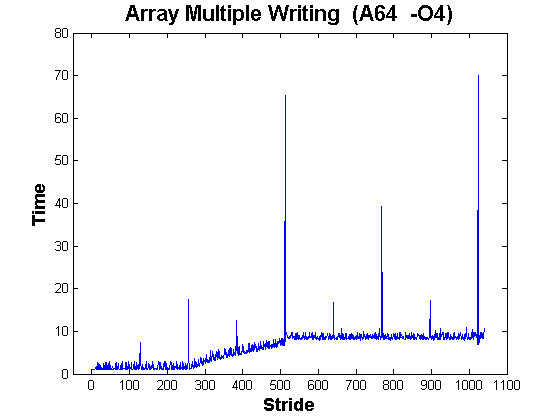
and here are the 32-bit AMD results:
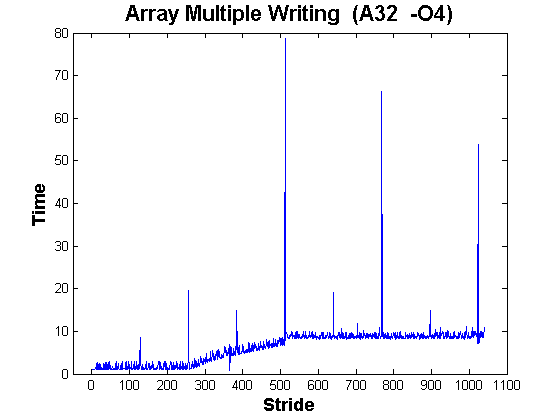
Sadly, the peaks are still present. Large strides are still worse than small strides by nearly an order of magnitude. And the size of the peaks is astonishing, up to 70x.
CYCLES c; #define N 1000000 double a[N], b[N], c[N]; long long t; for( int i=0; i<N; ++i ) a[i] = b[i] = c[i] = 1.0; // initialize c.tic(); for( int i=0; i<N; ++i ) a[i] = b[i] + c[i]; t = c.toc();for the case of three arrays, and
CYCLES c;
#define N 1000000
struct three { double a, b, c; } A[N], *p;
long long t;
int i;
for( i=0, p=A; i<N; ++i, ++p )
p->a = p->b = p->c = 1.0; // initialize
c.tic();
for( i=0, p=A; i<N; ++i, ++p )
p->a = p->b + p->c;
t = c.toc();
for the structure case. Just to see whether the order matters, we can also
measure
p->c = p->a + p->b;Here are the results for the AMD 64-bit machine, with the programs compiled unoptimized:
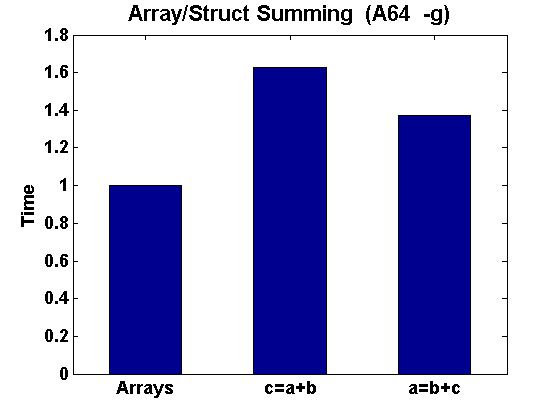
Note that using unit stride with separate arrays is significanly faster than the structure cases, by tens of percents. Note also that there is a significant difference between the two structure cases, depending on the data ordering in the structure. If we optimize, we get
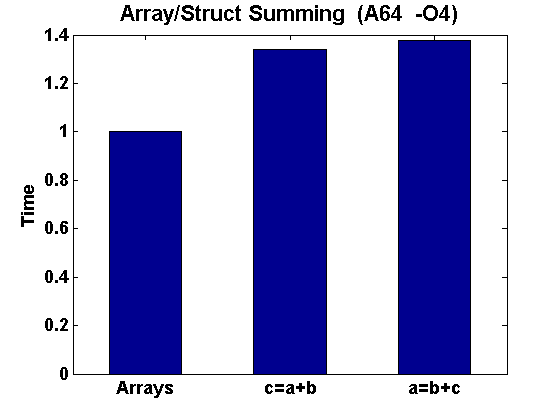
Once again, using separate arrays is significantly faster than using structures. The order of the data in the structure is much less important when the program is optimized.
I have collected too much wrong performance data in my career not to warn that these data may contain artifacts and noise due to operating system tasks and other background computing. More seriously, with just a few tests we are far from understanding the effect of CPU speed, cache size and architecture, and memory system architecture on the performance of even these simple programs. There is enough data, however, to strongly suggest that modern computer cache/memory systems do not reward locality of reference, but rather reward sequential access to data. The data also suggest that access patterns that jump by powers of two can pay a surprisingly large penalty. Those doing 2-D FFT, for example (where powers of two have long been touted as more efficient than other sizes) may wish to take notice.
I am not trying to suggest that computers have not been designed well for the typical tasks they they perform (e.g., running Apache, Firefox and Microsoft office). However, with 64-bit computers and terabyte datasets becoming common, computation on data that greatly exceeds the cache size is becoming a frequent experience. It is unclear how such data should be organized for efficient computation, even on a single-processor machines. With multicore upon us, designing for large data gets even more murky.
It is tempting to think that there is some way to organize data to be efficient on these machines. But this would imply that the system designers were aware of these issues when the machines were designed. Unfortunately, that may well not have been the case. History shows that computing systems are often designed by engineers more motivated by cost, chip and board area, cooling, and other considerations than programmability. Future data structure design, especially for large data, may well end up depending on the cache and memory sizes, number of cores, and the compiler technology available on the target system. "Trial and error" may have to prevail when designing data structures and algorithms for large-data applications. The old rules no longer apply.
We can speculate that "large data computing" could become a niche market, similar to the markets for servers and low-power systems. Perhaps we can work with hardware manufacturers to develop techniques for algorithm and data-structure design that software designers can follow, and hardware manufacturers can efficiently support. Meanwhile, try this at home, and welcome to a brave new world.
There is an interesting book by David Loshin, Efficient Memory Programming, which has a lot of material on how caches and memory systems work (even though the book dates from 1998). Unfortunately, there isn't a lot of empirical data, and he repeats the old saws about locality of reference.
There is also a field of algorithm design called Cache Aware Algorithms. The idea is to develop a family of algorithms to solve a particular problem, and then choose one that best fits the machine you are running on. While this is an effective technique, it begs the question of how we design data structures to optimize performance for today's machines. Google "cache aware algorithm" to learn more than you want to know about this field.
It's worth pointing out that similar issues arose once before in the vector machine era (1975 to 1990 or so). Vector machines so preferred unit stride that many powerful compiler techniques were developed to favor unit stride. It is also notable that most vector machines did not have caches, since reading and writing long vectors can "blow out" a conventional cache while getting little benefit thereby.
Here is the detailed information about the machines I used to collect this data.